Details of the Golden Ratio are explained through below points:
1. Historical Background
2. Golden Ratio
3. Construction of Golden Rectangle
4. Examples of Golden Ratio
1. Historical Background:
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. Expressed algebraically:

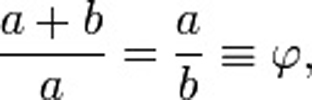
where the Greek letter phi ( ) represents the golden ratio. Its value is:
) represents the golden ratio. Its value is:
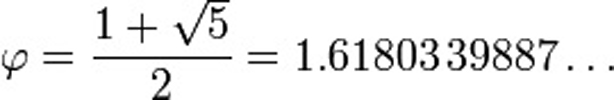
The golden ratio, or phi, was first understood and used by the ancient mathematicians in Egypt, two to three thousand years ago, due to its frequent appearance in Geometry. Phidias (500BC-432 BC), a Greek sculptor and mathematician, studied Phi and used it in many designs of his sculptures, such as the statue of the goddess Athena in Athena, and the state of god Zeus in Olympiad. In the Elements, the most influential mathematics textbook ever written, Euclid of Alexandria (ca. 300 BC) defines a proportion derived from a division of a line into what he calls its "extreme and mean ratio." Euclid's definition reads:
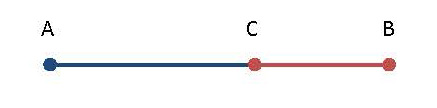
A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the lesser.
In other words, in the diagram below, point C divides the line in such a way that the ratio of AC to CB is equal to the ratio of AB to AC.
The name "Golden Ratio" appears in the form section area (Golden Section in Greek) by Leonardo da Vinci (1452-1519) who used this Golden ratio in many of his masterpieces, such as The Last Supper and Mona Lisa.
In 1900s, a Maerican mathematician named Mark Barr represented the Golden Ratio by using a Greek symbol Φ (phi).
2. Golden Ratio:
The golden ratio is obtained by dividing any term of the Fibonacci sequence by its preceding number. It has a value approximately equal to 1.618 and is also known by terms as golden section, golden mean, extreme and mean ratio, medial section, divine proportion, divine section, golden proportion, golden cut, golden number, mean of Phidias etc.
The geometric spiral and the geometric rectangle are two of the most important constructs derived from the golden ratio. A golden rectangle has its height and width in the golden ratio whereas a golden spiral is a logarithmic spiral whose growth factor is the golden ratio. Other important constructs are the golden triangle and golden ellipse. The golden triangle is an isosceles triangle with an angle of 36 degrees at the vertex and base angles equal to 72 degrees each.
3. Construction of Golden Rectangle:
• 3a - Using Square Construction Method
• 3b - Using Triangle Construction Method
• 3a. Using Square Construction Method:

1. Draw a square

2. Draw a diagonal from mid-point A of one of the sides to an opposite corner B. With A as the centre, draw an arc to cut the side at C. Draw a perpendicular from C to get the golden rectangle.
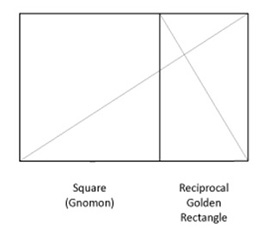
3. The golden rectangle can be subdivided as shown. When subdivided, it produces a smaller proportional golden rectangle called the reciprocal, and a square area called the gnomon remains after subdivision.
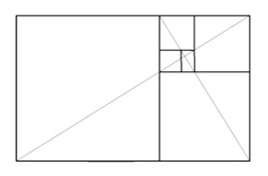
4. The process of subdivision can go on, producing smaller proportional rectangles and squares.
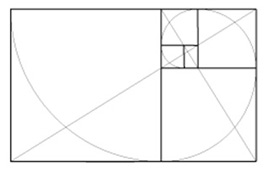
5. The proportionally decreasing squares can further produce a spiral by using a radius equal to the length of the sides of the square.
6. The squares from the golden section subdivision section are also in golden proportion to each other.
• 3b. Using Triangle Construction Method:
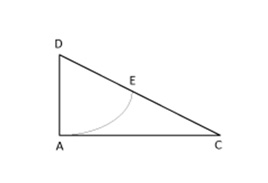
1. Draw a right triangle whose sides are in the ratio 1:2. Using D as centre and DA as radius, draw an arc that cuts the hypotenuse at E.
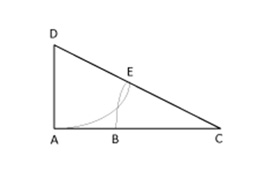
2. With C as centre and CE as radius, draw another arc that cuts AC at B.
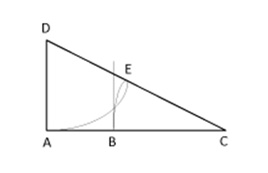
3. From B, draw a perpendicular to DC.
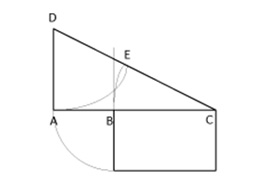
4. AB and BC are in the golden proportions and the subdivision of the triangle yields sides of a rectangle in golden ratio proportion.
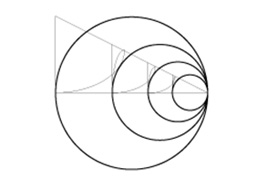
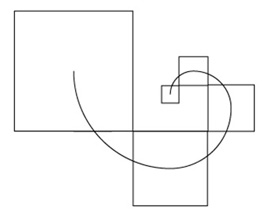
Apart from the golden rectangle, the triangle construction method produces a series of circles and squares that are in golden section proportion to each other.
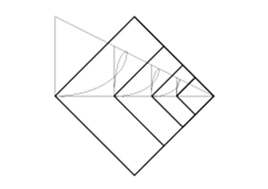
Apart from the golden rectangle, the triangle construction method produces a series of circles and squares that are in golden section proportion to each other.
4. Examples of Golden Ratio:
• 4a - In Nature
• 4b - In the Human Body
• 4c - In Art and Architecture
• 4d - In Music
4a. In Nature:
If one looks at the array of seeds in the center of a sunflower, he can notice what looks like spiral patterns curving left and right. Amazingly, on counting these spirals, the total will be a Fibonacci number. Dividing the spirals into those pointed left and right, we'll get two consecutive Fibonacci numbers. Similar spiral patterns in pinecones, pineapples and cauliflower that also reflect the Fibonacci sequence can be deciphered in this manner.
Below are images of cross-sections of a Nautilus sea shell. They show the spiral curve of the shell and the internal chambers that the animal using it adds on as it grows. The chambers provide buoyancy in the water.
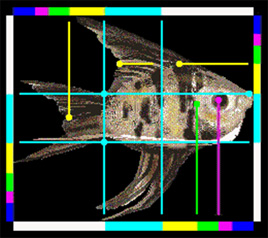
Angel Fish - Every key body feature of the angel fish falls at golden sections of its width and length. The nose, tail section, and centers of the fins of the angel fish fall at first (blue) golden sections. The second golden section (yellow) defines the indents on the dorsal and tail finds as well as the top of the body. The green section defines the marking around the eye and the magenta section defines the eye. (Source: goldennumber.net)

Some plants express the Fibonacci sequence in their growth points, the places where tree branches form or split. One trunk grows until it produces a branch, resulting in two growth points. The main trunk then produces another branch, resulting in three growth points. Then the trunk and the first branch produce two more growth points, bringing the total to five. This pattern continues, following the Fibonacci numbers.
(Source: journalofcosmology.com)
4b. In the Human Body:
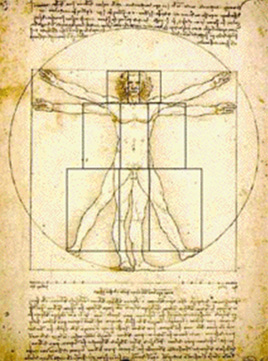
The Vitruvian Man is a world-renowned drawing created by Leonardo da Vinci circa 1487. A square encloses the body while the hands and feet touch a circle with the navel as center. The figure is divided in half at the groin, and by the golden section at the navel. The drawing is based on the correlations of ideal human proportions with geometry described by the ancient Roman architect Vitruvius in Book III of his treatise De Architectura.
(Source: sistertongue.wordpress.com)
From the illustration given below, we can see several occurrences of the golden ratio found in the human body.
1. Sole to navel: Sole to crown.
2. Sole to knee: Sole to navel.
3. Navel to shoulder: Navel to crown.
4. Knee to calf-muscle: Knee to sole.
5. Navel to mid-thigh: Navel to knee.
6. Navel to mid-chest: Navel to base of throat.
7. Base of throat to temple: Base of throat to crown.
8. Calf muscle to ankle: Calf muscle to sole.
9. Mid-thigh to start of kneecap: Mid-thigh to end of kneecap.
10. Navel to crotch: Navel to mid-thigh.
11. Navel to sternum base: Navel to sternum or mid-chest.
12. Base of throat to earlobe: Base of throat to top of ear.
13. Brow bone to hairline: Brow bone to crown.
14. Nose to chin: Nose to base of throat
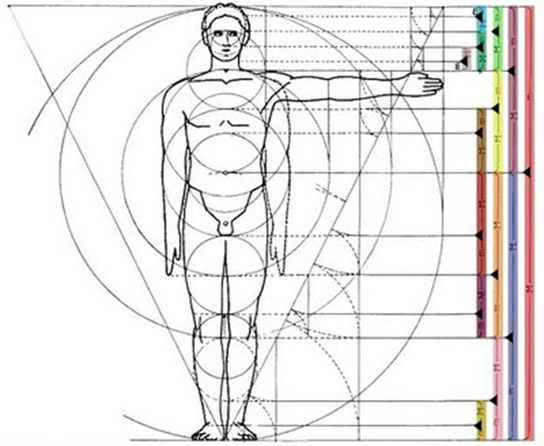
(Source: beautifulproportion.com)
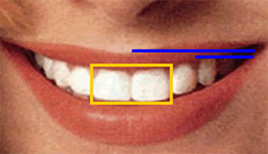
For a perfect smile, the front two teeth form a golden rectangle. There is also a golden ratio in the height to width of the center two teeth. And the ratio of the width of the two center teeth to those next to them is phi. The ratio of the width of the smile to the third tooth from the center is also phi.
(Source: library.thinkquest.org)
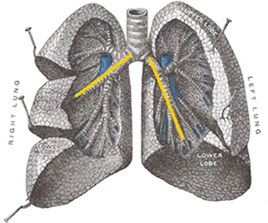
In the human lungs, the windpipe divides into two main bronchi, one long (the left) and the other short (the right). This asymmetrical division continues into the subsequent subdivisions of the bronchi. It was determined that in all these divisions the proportion of the short bronchus to the long was always 1/1.618.
(Source: library.thinkquest.org)
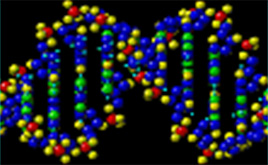
Even the DNA molecule, the program for all life, is based on the Golden section. It measures 34 angstroms long by 21 angstroms wide for each full cycle of its double helix spiral.34 and 21, of course, are numbers in the Fibonacci series and their ratio, 1.6190476 closely approximates Phi, 1.6180339.
(Source: sites.google.com/site/chsscience/)
4c. In Art and Architecture:

Mona-Lisa by Leonardo da Vinci
(Source: sinearch.com)

Holy Family by Micahelangelo
The principal figures are in alignment with a pentagram or golden star.
(Source: fabulousfibonacci.com)

Self-portrait by Rembrandt
The triangle cuts the base in the golden section.
(Source: jwilson.coe.uga.edu)

The sacrament of the Last Supper
-by Salvador Dali
The picture is painted inside a golden rectangle.
(Source: goldennumber.net)

Parthenon
(Source: britton.disted.camosun.bc.ca)

The Great Pyramid of Giza
(Source: jwilson.coe.uga.edu)

Statue of Athena
(Source: library.thinkquest.org)
4d. In Music:
In addition to existing in nature, art and architecture, it has been hypothesized that great classical composers like Mozart had an awareness of the Golden Ratio and used it to compose some of his famous sonatas. The Golden Ratio appears in the relationship of the intervals or distance between the notes. Musical scales are based on Fibonacci numbers. There are 13 notes in the span of any note through its octave. A scale is comprised of 8 notes, of which the 5th and 3rd notes create the basic foundation of all chords, and are based on whole tone which is 2 steps from the root tone, that is the 1st note of the scale.





